В DV-2019 не могут принимать участие уроженцы государств, общее население которых по самым грубым подсчетам превышает 4 млрд 100 млн человек. Это около 54-55% всего населения Земли (сейчас примерно 7 млрд 550 млн человек). Еще около 4,3% населения Земли в принципе не нуждаются в участии в лотерее (постоянные жители и граждане США).
Если бы вдруг в лотерее отменили ограничитель на участие уроженцев стран с большой иммиграцией в США, то шансы всех участников DV-2019 внезапно упали бы более чем в 2 раза!
Так что на нынешнее положение дел грех жаловаться… 
Ура!
А это правда, что с американского IP чуток выше шанс?
Среди знакомых победителей заметил тенденцию - кто играет из США (по тур поездке даже) - выигрывают.
звучит бредово, но мало ли, послушаем экспертов.
Причем тут именно DV-2019?
Так всегда было, это одно из изначальных условий лотереи, не допускаются к участию страны, превысившие лимит иммигрировавших за последние пять лет.
Конечно нет.
Разве в моем посте это как-то опровергается? Я просто взял список стран, уроженцы которых не допущены к участию к DV-2019, и посчитал их население. Почему именно DV-2019? Да потому что DV-2018 уже прошла, а DV-2020 даже не назначена. А список ineligible стран обновляется каждый год. Например, начиная с DV-2010 из него выпала россия, а c DV-2018 — Эквадор.
Ну всё, замотивировался по самые помидоры :).
Средняя вероятность выигрыша - около 1%. Вероятность, что вы выиграете на десятом участии подряд в лотерее - так же 1%. Так что оптимизм оптимизмом, а взяли себя в руки, заполнили заявку, поставили напоминание на телефоне и забыли до проверки результатов.
Это не совсем так.
Давайте разберемся с вероятностями вместе. Пусть вероятность выигрыша всегда будет p. Одновременно это означает, что вероятность невыигрыша — 1–p.
Вероятность не выиграть два года подряд, это вероятность не выиграть при условии состоявшегося проигрыша в первый раз. Такие вероятности перемножаются. То есть, вероятность не выиграть два года подряд = (1 – p)(1 – p) = (1 – p)^2.
Легко посчитать вероятность проигрыша N лет подряд — (1 – p)[1]N[/i].
Но тогда вероятность выиграть хотя бы один раз (а нам ведь больше и не надо, да?) за N лет будет вовсе не p, а 1 – (1 – p)[2]N[/i].
Давайте посчитаем такую вероятность, например, для России.
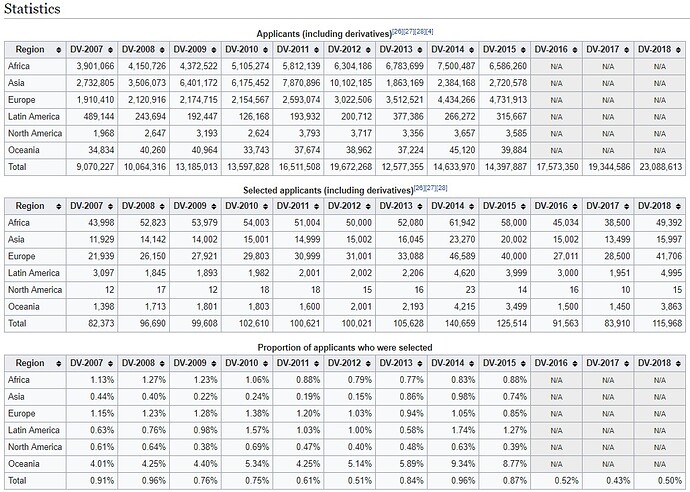
Согласно имеющейся статистике, от России в DV-2015 было подано 131202 заявки (265086 человек вместе с членами семьи). Отобрано было 4103 человека. Из пропорции заявок и количестве перечисленных в заявках людей можно предположить, что 2031 заявитель от России был уведомлен о выигрыше.
То есть вероятность выигрыша одной заявки составила 1,5% (точнее мне не нужно). Это значит, что вероятность проигрыша одной заявки составила 98,5% (0,985).
Если предположить, что в течение десяти лет вероятность выигрыша одной заявки не изменится (очень умозрительное умозаключение, но лучше-то всё равно нет), то вероятность не выиграть на протяжении 10 лет будет
1 – 0,985^10 = 0.86. То есть, вероятность выиграть хотя бы один раз в течение 10 лет равна 14%.
Если речь идет о семье, то в ней как правило подаются минимум две заявки! Это значит, что вероятность проигрыша обеих заявок одновременно в одном году составит 0,985*0,985 = 0,97. Вероятность того, что ни одна заявка семьи не выиграет ни одного разу за 10 лет, будет уже 73,9%.
Итого, шансы в течение 10 лет выиграть хотя бы одну заявку на семью повышаются до 26%.
Вышеприведенные рассуждения не означают, что если Вы играли предыдущие 9 лет безрезультатно, то в этом году вероятность выигрыша вдруг подскакивает до 26%. Отнюдь нет. Она как была 1,5%, так и осталась 1,5%. Ведь все предыдущие годы теперь не условия, а состоявшийся факт.
Речь шла лишь о высказывании, на которое я дал свой комментарий. Я понял так, что речь идет о человеке, который собрался играть и перед которым 10 будущих лет участия. В такой ситуации можно утверждать, что с вероятностью 14% ему выпадет выигрыш в ближайшие 10 лет. И не больше.
…Это при условии идеальной подачи идеальной заявки, т.е. когда успех или неуспех зависит исключительно от Фортуны. Однако же при иных обстоятельствах, если заявки из года в год оказываются попросту дисквалифицированными, всё это теряет смысл. И утверждение, что мол “ты выиграешь хоть раз в течение ближайших 10 лет с шансами 1 к 7” окажется неправдой, если, например, у человека есть недоброжелатель, подающий заявки от его же имени и с его фотографиями из года в год. Тогда его шансы на выигрыш будут равны 0 и в конкретном розыгрыше, и в течении любой последовательности розыгрышей. И правды мы никогда не узнаем.
Весь оптимизм мой народу испортил… ![]()
Абсолютно верно. 15 лет прошло с моего институтского курса Теории Вероятности. И как и сказано ранее - вероятность выиграть примерно такая же, как и 10 лет назад ![]()
Плюс много непроверяемых случайностей, отклоняющих анкету даже в случае с выигрышем.
И как вам сказали ранее - не рассказывайте никому о своем намерении - что бы кто то просто вам не подгадил, отправив анкету от вашего имени.
Ну мы старались ![]()
Ого а почему такая большая разница у Азии между 2012 и 2013 годами, на 9 млн меньше заявок?=0
Перестали принимать заявки от Бангладеш.
А откуда у недоброжелателей фото возьмется?
Ну… например некто заключил договор с посреднической конторой, обещающей ему “бескоштовий” переезд в Америку, а потом передумал и расторг договор. Договор-то расторгнут, а фоточка-то осталась! И это только одна из схем пополнить карманы за счет людей, грезящих об American dream.
Зачем вообще было заключать договор с такой конторой?
Люди сначала делают глупости, а потом удивляются, почему все идет не так, как хотелось бы.
У некоторых заявок вместо HNBS выдается ошибка, значит их удалили, а раз удалили, значит что-то с ними было не так…
например Confirmation number неправильно набран. А еще фамилия с именем местами перепутаны или год неправильно набран. Полагаю эти три причины закрывают 100% выдачи ошибок.
Примите людей такими, какие они есть. Если бы люди не ошибались, то это были бы боги.